It is shown that a surface of porous material or auditorium seats yields negative reflection at the grazing angle1). It is also mentioned2) that the reflection from the front seats at an amphitheater is less because of their steep angle (26.3 degrees) and that its path deference from the direct sound from the stage is larger than at the grazing angle.
These discussions were done when the surface is flat. Here it is discussed on the effect of the curvature of a surface.
1) Sound reflection at the grazing angle
Reflection coefficient was defined for a surface which is not rigid and it was measured with a large panel of the surface. It was used to get the reflection of a limited dimension with the surface to be convolved to the rigid panel of the dimension.
Thus defined reflection coefficients of two different porous surfaces are show in Fig.1. They are for a punch carpet layer and a urethane foam layer.
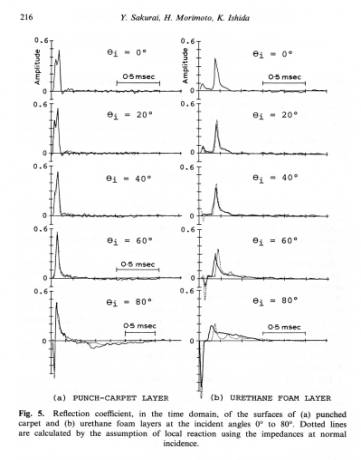
Fig.1 Reflection coefficients of two porous layers
It has a positive surface reflection at the normal incidence but it shows a large negative surface reflection at 80 degrees which is close to the grazing angle.
An apparent surface was given as shown in Fig.2 for uneven auditorium seats. A reflection coefficient was measured at the ear position for an audience. An incident angle is shown by θi. They are for hard and absorptive seats in Fig.2.
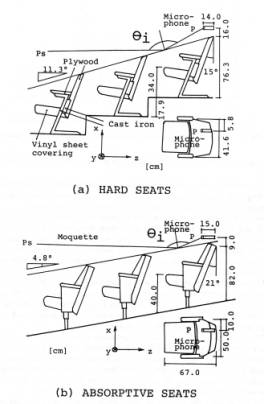
Fig.2 Apparent surface of auditorium seats and a receiving point for the reflection coefficient measurement
Thus measured reflection coefficients of auditorium seats at the grazing angle for world famous concert halls are shown in Fig.3. They are shown in the time and frequency domains. Fig.4 shows the sketches of their auditorium seats.
The first negative reflection coefficients are gathered in Fig.5 with a few additions of Japanese auditoriums.
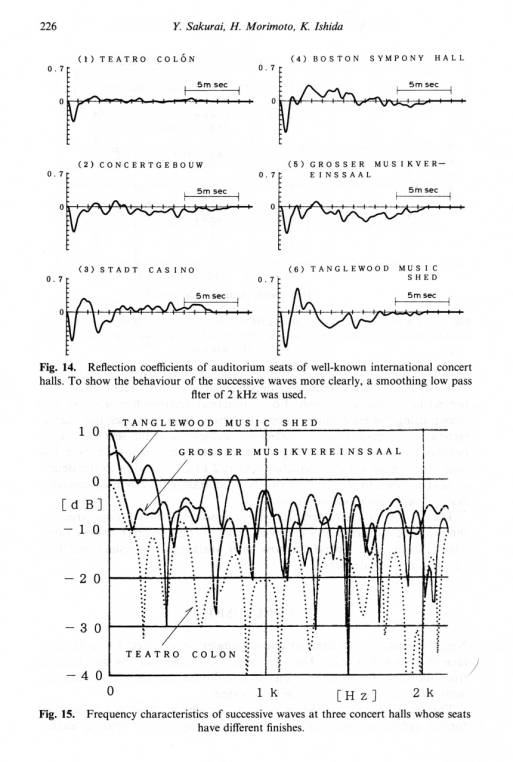
Fig.3 Reflection coefficients of auditorium seats at six world famous concert halls in the time and frequency domains
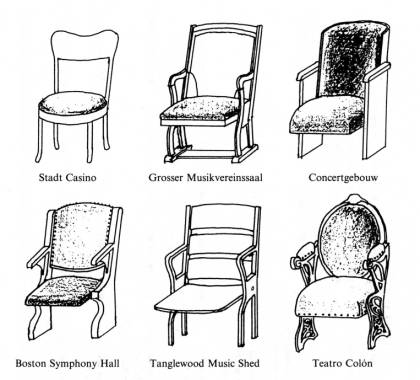
Fig.4 Sketches of auditorium seats of the six concert halls
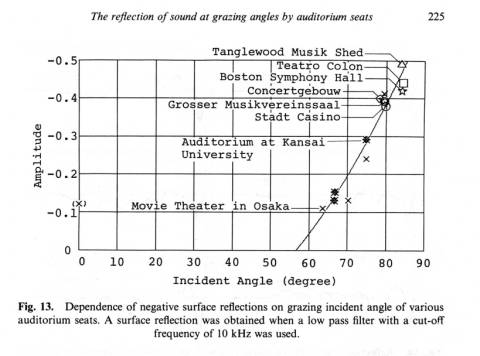
Fig.5 Incident angles and first surface reflections of auditorium seats at world famous concert halls and a few Japanese auditoriums
While, a Greek amphitheatre has a slope with 26.3 degrees, as shown in Fig.6. The angle refers to around 65 degrees in Fig.5, where the reflection coefficient is smaller in negative.
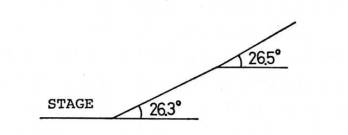
Fig.6 Steep slope of audience seats at a Greek amphitheater
In this way, a Greek amphitheatre has commonly the audience slope of 26.3 degrees and they get the direct sound from the stage very clear.
2) Reflection from a rigid concaved surface
To have the reflection of a concaved surface it was divided into small rectangles where each of them gets plane wave incidence and it was summed up being calculated by the Fraunhofer equation. The reflection from each rectangle has a pair of positive and negative rectangular waves from the far field term and a trapezoid wave from the near field term as shown in the above of Fig.7.
In the below of Fig.7, it is shown how they are summed for a concave and convex surfaces. For a concave surface, the reflection from each rectangle is in phase with the one of the rectangle at the specular reflection and they compose a pair of large and negative reflections.
For a convex surface, the positive pair remains but the negative pair is cancelled with the positive pairs of the surrounding rectangles. So it tends to remain only a positive reflection from the rectangle of the specular reflection and it is affected by the curvature.
In fig.8, two examples are shown compared with experimental results. The successive multiple reflections are not calculated but they simulate the specular reflection well.
Fig.9 shows the calculated reflection of a concaved surface when its curvature is changed. Specular reflection is very large with the addition in phase and its spectrum is large too. In this condition, the amplitude and spectral level are largest at the curvature Rc 70cm.
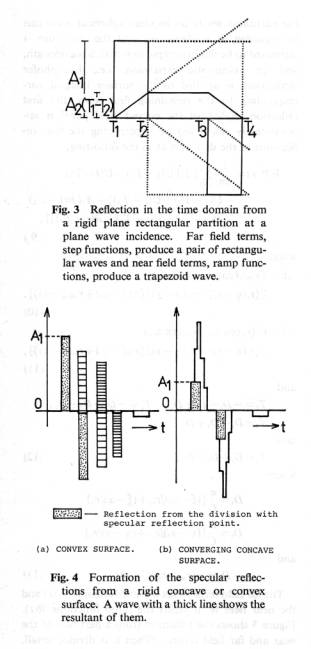
Fig.7 Reflections from a divided rectangle in the above and the addition of reflections of the surrounding rectangles to the specular reflection in the below
The reflection of a convex surface is given in the left and that of a concave surface in the right.
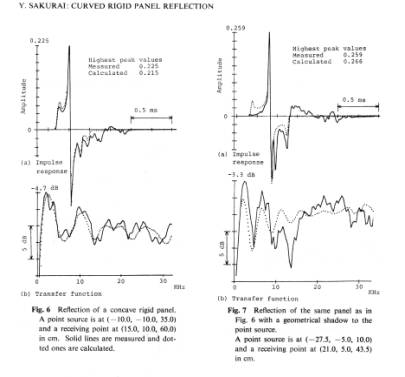
Fig.8 Comparison of a calculated and measured result for a concave surface
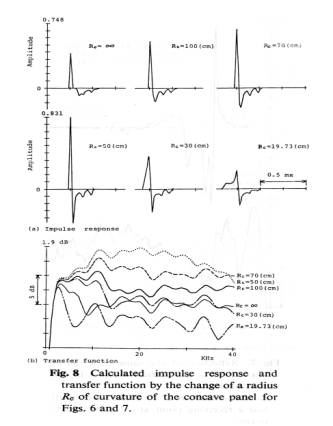
Fig.9 Reflection of a concaved surface with the change of its curvature
Thus, the negative reflection from the front seats becomes small and delayed because of the steep slope, and the received level is amplified by the curvature at the audience.
It is possible to have an impulse response at an audience with the practical dimensions of an amphitheatre. It should be convolved with the transient response of our hearing system and integrated in the time window after absolutization.
3) Another possibility which makes amphitheatre acoustics good
It has been discussed only for the direct sound from the stage but it needs a bit of reverberation.
The impulse response for the curvature Rc 70cm in Fig.9 shows a large specular reflection with ± amplitude and a successive transient wave after them. It is given from the area surrounding the specular reflection rectangles with delayed reflections. They are imagined to add a bit of reverberation.
Further discussion should be done after the transient response of our hearing system is convolved, comparing with the reflection at a usual auditorium seats.
4) Rectangular reflectors surrounding the stage
There are wooden rectangular panels at the three sides on the stage to support performers as can be seen in the later photos. To show the acoustical difference, I spoke or sang outside or inside the enclosure, they recognized it very clearly.
It was clearly noticed too from the stage when audience talks back to me. It is reciprocal.
It is apparent that the rectangular enclosure gives a good support to the performers on the stage. Rich normal modes are created by the enclosure. How would it be if a ceiling is added to get richer normal modes or the dimensions of reflectors are changed referring to the musical notes? Interesting questions are never finished.
Summery
An impulse response at an audience from a sound source on the stage of rectangular enclosure, which is the direct sound, can be calculated. The sound reflected by the front audiences can be calculated by the convolution of the reflection coefficient and the reflection of the concaved surface. Then the impulse response at an audience is obtained by the addition of them.
The evaluation of the sound field can be done there and after the transient response of our hearing system is convolved.
It is not difficult to get such slopes in the green country NZ. It is very lucky to be able to enjoy music and/or plays in the green space under the stars. We held music gatherings ten times once in a year in March celebrating autumn harvests. If this kind of event would be expanded, it would be wonderful. A few photo shots are given below.
References
1)Y. Sakurai and K. Nagata, “Practical estimation of sound reflection of a panel with a reflection coefficient” , J. Acoust. Soc. Jpn (E), 3, 1, p7-19 (1982)
2) Y.Sakurai, H.Morimoto and K.Ishida,” The reflection of sound at grazing angles by auditorium seats”, p209-227, Applied Acoustics 39(1993).
3) Y.Sakurai,” The early reflection of the impulse response in an auditorium”, p127-138, J.Acoust.Soc.Jpn.(E), 8, 4(1987).
4) Y.Sakurai, ”Sound reflection of a curved rigid panel”, p63-70, J. Acoust. Soc. Jpn(E), 2, 3(1981).
5) Y.Sakurai and H.Morimoto,” The transient response of human hearing system”, J.Acoust.Soc.Jpn.(E), 10, 4(1989).
Photos from handmade music gatherings





