Yoshimasa Sakurai
Experimental House, Gibbons Rd, RD2, Kaiwaka, NZ, and
Hiroshi Morimoto
Suisaku Ltd, 21-1 Mihara-cho, Kotera, Minami kawachi-gun, Osaka, Japan
1. INTRODUCTION
It is important for noise control to find out how sound diffraction is affected depending on the arrangement of noise barriers. A semi-infinite barrier needs a heavy structure to build and if it is constructed for a house, it should be extended long enough. It is interesting to see the difference in diffraction when it is surrounded by a U-shaped barrier or a closed barrier. A house has certain dimensions, however, in this paper it is discussed how sound pressure is transferred to a single receiving point inside the barrier.
2. The half amplitude method
If diffraction is expressed in the frequency domain only with amplitude there is no way to have the total diffraction from each part of the barrier. However, if the diffraction is expressed in the time domain, the diffraction from the whole barrier can be obtained by the addition of the effect of each part using the half amplitude method 1)2).
The following equation expresses the sound field around a semi-infinite wedge in Fig.1 by Biot & Tolstoy3)
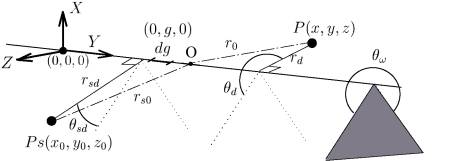
Fig.1 Diffraction around a semi-infinite wedge
where c is sound velocity, Sis a signal power and ρ is medium density. Parameter Y and β are;
Where t is time, and
For the details of Eq.(1), see reference3).
The equation tells us that it is the line source along the ridge giving the first and largest contribution from the point O on the ridge along the shortest path and that after the point the equal amplitude is given to the receiving point simultaneously from each side of the ridge. It means that when a wedge has a finite length, half the amplitude is lost at the first end and another half at the other end as shown in Fig.2
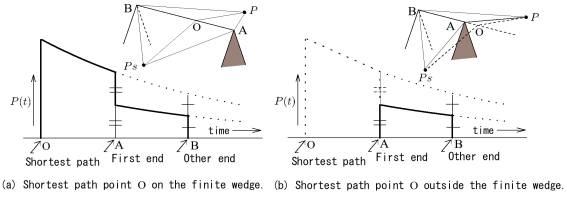
Fig.2 Diffraction of a finite wedge
3. Noise barrier arrangement
In this paper, five arrangements of thin barriers as shown in Fig.3 are discussed. (i) is a semi-infinite barrier, (ii) is a U-shaped barrier with two semi-infinite side barriers, (iii) is the one with two finite side barriers, (iv) is a closed rectangular barrier and (v) is similar but the side barrier has a double length of (iv). The length of the barrier AB is the same for each arrangement, and a point source Ps1 and a receiving point P are at the same places along the barrier AB. Geometrical dimensions are given in the figure.The height of the point source Ps1 is 1m and that of the receiving point P is 0.5m lower than the height of the barrier.
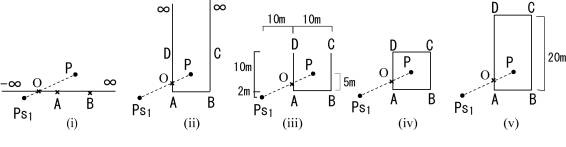
Fig.3 Arrangement of barriers
The impulse response of the semi-infinite barrier is explained using the half amplitude method in Fig.4.
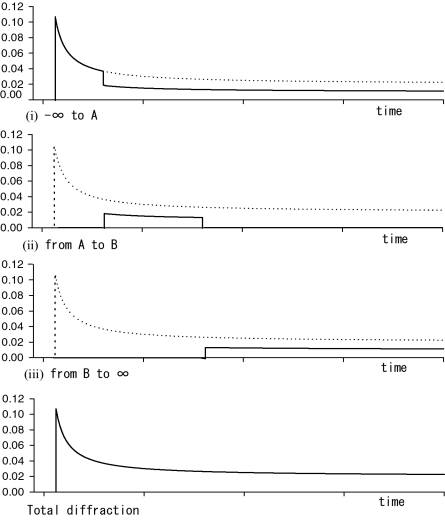
Fig.4 Diffraction of the semi-infinite thin barrier using the half amplitude method when a sound source is at Ps1.
4. Diffraction calculation for each arrangement
(4-1) Time domain
The main interest is to find how the diffraction and the reflection by both side barriers and the rear wall occur when they are compared with the diffraction of the semi-infinite barrier.
The diffraction over the barrier AD and the barrier AB in Fig.3 (ii) or (iii) is the first direct diffraction to the receiving point when a point source is at Ps1. After this, the sound diffraction over the barrier AD produces the geometrical and the edge reflections at the barrier BC and the edge reflection at the barrier AB as shown in Fig.5, and similarly the barrier AB produces reflections at the both side barriers AD and BC.
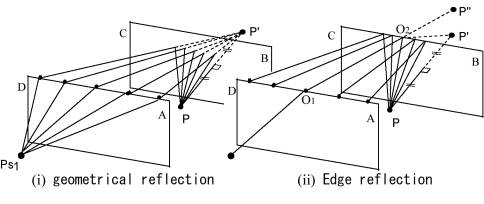
Fig.5 Geometrical and edge reflections at the barrier BC for the diffracted wave over the barrier AD.
The geometrical reflection for the barrier AD is calculated as the diffraction over the barrier to the image receiving point P’ along the projection of the edge of AD to the barrier BC, as is the diffraction over the barrier AB. In Fig.3 (iv) and (v), the barrier CD joins to produce reflections.
The edge reflection at the barrier BC of the diffraction over the barrier AD is calculated as the double diffraction, though the second one is actually reflection. First, the shortest path between Ps1 and P’ over the edges of AD and BC is found. When the crossing point on the edge CD is O1, and the one on the edge BC is O2, P” is located at the extension of the path O1O2 with the distance from O2 to P’. After the shortest path point O1, each side of the edge AD is divided into divisions in pairs whose paths give the same arriving time to P”. Now, each division with a half of the amplitude given by Eq. (1) is a point source for the edge reflection at the edge BC to the receiving point P. It is calculated by Eq. (1) as well. The contribution of each division is summed up and the edge reflection is obtained.
The calculations were done until the second order. The reflection of the ground was not included. If it is necessary, the same calculation can be done for the object in the air.
Calculated diffraction in the time domain is shown in Fig.6 for the different barrier arrangements, when a point source is at Ps1.
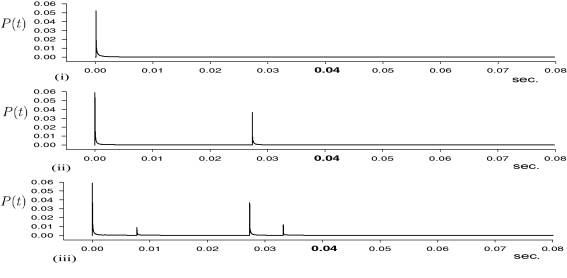
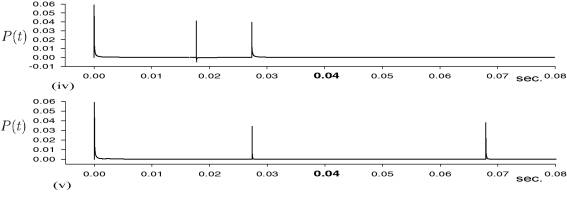
Fig.6 Calculated diffraction in the time domain for the different barrier arrangements in Fig.3 when a point source is at Ps1.
The shortest path from the point source Ps1 to the receiving point P for every arrangement from (ii) to (v) in Fig.3 crosses on the ridge of the barrier AD. It crosses before the point A on the semi-infinite barrier in Fig.3(i). Those points give the first and largest peaks in the diffraction and the one from the semi-infinite barrier is a little less in the amplitude than the other barriers.
The next dominant diffraction is the geometrical reflection on the barrier BC of the diffraction over the barrier AD. At the estimation of calculated results, the time pattern of traffic noise must be considered. However, we can say at least that it is essential to reduce the first diffraction over a barrier and the reflections at the other barriers.
In this situation, if a Helmholz resonator type absorbent is used at the barrier edge, it decreases the noise level behind it, because the line source there is convolved with its impulse response that oscillates in positive and negative. Therefore, it must be more efficient than porous absorbents.
(4-2) Frequency Domain
As the calculated result in the time domain has the dominant contribution from the
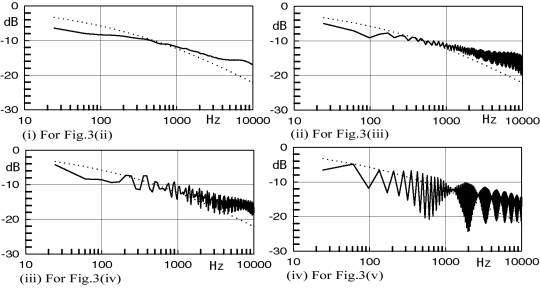
Fig.7 Transfer function of the diffraction for each arrangement in Fig.3(ii) to (v) being compared with the one for the semi-infinite barrier
shortest path, which includes high frequency components, it is difficult to notice how the change in the low frequency occurs because of the low and long gradual decrease. The transfer function for each arrangement from (ii) to (v) in Fig.3 is shown by a continuous curve in Fig.7 being compared with the one by a dotted line for the semi-infinite barrier.
A further important aspect is that we have to estimate the perceptive noise level after the integration during the time window, which is assumed 40msec, of the absolute value after a practical noise is convolved with the impulse response of the barriers and the transient response of our hearing system4).
Discussions
When two fences meet and make a corner, the diffractions of each fence there are different. They should be the same. This was caused by further multiple diffractions, and they need the help of the boundary integral equation in the time domain to be compared and find the relation.
References
1)H.Morimoto & Y.Sakurai; ”Diffraction of a semi-infinite thick barrier”, to be published on the Journal of JASJpn (in Japanese).
2)H.Morimoto & Y.Sakurai; ”Diffraction around a rectangular body”, to be published on the Journal of JASJpn (in Japanese).
3)I.Tolstoy; ”Wave propagation”, p.339-347, 1973, McGraw-Hill.
4)Y.Sakurai & H.Morimoto; ”Binaural hearing and time window in the transient”, J. Acoust.Soc.Jpn(E), 10, 4, p.229-233(1989).