This paper was given at the Acoustical Society of New Zealand in 2002 by
Yoshimasa Sakurai
Experimental House, 112 Gibbons Rd, RD2, Kaiwaka, NZ, and
Hiroshi Morimoto
Suisaku Ltd, 21-1 Mihara-cho, Kotera, Minami Kawachi-gun, Osaka, Japan.
Introduction
Using the half amplitude method, the diffraction of a semi-infinite thick barrier and a rectangular body was predicted quite well when they were compared with measured results 1). In this paper, the diffraction by a semi-infinite thick barrier of various top shapes is compared on the calculation by the half amplitude method. The estimation for these differences will be discussed on the loudness estimation with the proposed formula, which is the logarithmic scale of the integration in the time window of the absolute value of the convolution of a sound and the transient response of the human hearing system 2).
A) Half amplitude method
The diffraction of a semi-infinite wedge was expressed by Biot-Tolstoy for the step function input. The expression was modified by Medwin for the impulse response. The equation behaves similarly to the first diffraction of a line source along the wedge 3). It was concluded from the similarity of the directivity of the peak value on the impulse response and the parallel shift in the transfer function. The shortest path point on the wedge from a point source to a receiving point gives the largest contribution. The same contribution is given at the same time from the segment in each side of the shortest path point on the wedge, where they have the same paths from the source to the receiving point.
Using this diffraction character of a wedge, the point source strength of a segment on the first wedge is obtained by the de-convolution of the distance term and the division by two. It is now the new point source for the next wedge. This method of the double diffraction calculation is called the half amplitude method 4).
B) Diffraction of a semi-infinite thick barrier with various top shapes
B-1) Diffraction of a semi-infinite thin barrier depending on its inclination
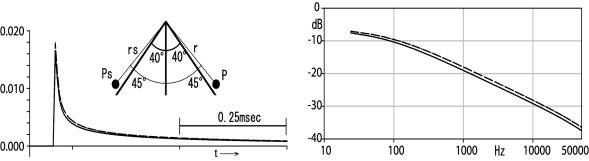
The diffraction of a semi-infinite thin barrier is shown in Figs.1, when it is inclined 40 degrees toward a point source or a receiving point. The distance from the point source to the barrier top and that from the receiving point are expressed by rs and r, respectively. Fig.1 shows when rs and r are equally 100cm and the point source is at (-70.71, 0.0, 70.71) in cm and the receiving point is at (-70.71, 0.0, -70.71) in cm. When the barrier is inclined to the point source and the receiving point, the diffraction is the same because of the sound field’s reciprocality.
(i) Impulse response (ii) Transfer function
Fig.1 Diffraction of a semi-infinite thin
barrier inclined 40degrees toward the point source or the receiving point,
being compared with that of the vertical one.
rs and r are 100cm. The
diffraction over the vertical barrier is shown by a continuous line, that of
the barrier inclined 40degrees toward the point source and the receiving point is
shown by a dotted line.
The peak value is only slightly more when the barrier is inclined. The inclination does not give any advantage for noise reduction.
B-2) Diffraction of a semi-infinite wedge when the wedge angle is changed
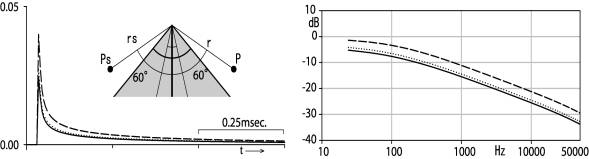
The diffraction of a semi-infinite wedge is calculated for a few wedge angles as shown in Fig.2, when the distances rs and r are equally 100cm.
(i)Impulse response (ii) Transfer function
Fig.2 Diffraction of a semi-infinite wedge
for a few wedge angles
rs and r are 100cm. Continuous
line shows of a wedge angle 0degree, a dotted line does of a wedge angle
30degrees and a chained line does of a wedge angle 90degree. The diffraction is mainly decided by the inclination of the source side panel 3). It might give a suggestion how to use the diffraction of the first wedge to the next wedge.
B-3) Diffraction of a semi-infinite thick barrier whose width is changed keeping the height same as that of the semi-infinite thin barrier
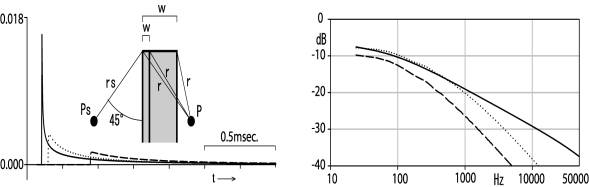
The diffraction of two semi-infinite 10cm and 50cm thick barriers is shown in Fig. 3, being compared with the diffraction of the semi-infinite thin barrier at the point source side surface. The distance rs from the point source to the first wedge is 100cm.The point source is fixed at (-70.71, 0.0, 70.71) in cm and the receiving point at (-70.71, 0.0, -70.71) in cm.
(i) Impulse response (ii) Transfer function
Fig.3 Diffraction of a semi-infinite thick
barrier of different thickness having the same height of the semi-infinite thin
barrier
Thickness is changed to 10cm and 50cm. The distance from the first wedge to the point source rs is 100cm. The diffraction over the 10cm thick barrier is shown by a dotted line and the one over the 50cm thick barrier is shown by a broken line, being compared with the diffraction over the vertical thin barrier at the front surface of the thick barrier for a continuous line.
The peak in an impulse response becomes lower as the thickness of a barrier becomes larger. Accordingly, it decreases high frequency components. However, the successive foot is not much changed by width.
In the transfer function, amplitude decrease is more in the whole frequency range by thickness increase. Especially the decrease in the low frequency for the 50cm thick barrier is meaningful for the practical point of noise control. It is consequently caused by the deeper location of the receiving point from the second wedge.
B-4) Diffraction of a semi-infinite thick barrier when a receiving point is moved by the thickness of the barrier
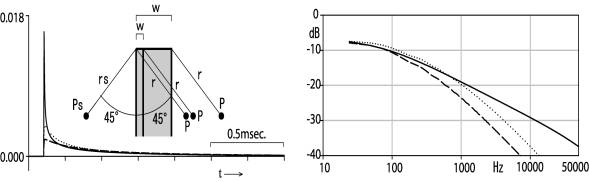
In the last section, a point source and a receiving point are fixed at the change of width. The diffraction of a semi-infinite thick barrier is compared when its thickness is changed and a receiving point is moved by the thickness as shown in Fig.4. A point source Ps is at (-70.71, 0.0, 70.71) in cm, and a receiving point P is at (-70.71, 00, -80.71) in cm for a 10cm thick barrier and is at (-70.71, 0.0. –120.71) in cm for a 50cm thick barrier.
(i) Impulse response (ii) Transfer function
Fig.4 Diffraction of a semi-infinite thick
barrier when a receiving point is moved by the thickness
rs and r are 100cm. The
diffraction over the 10cm thick barrier is shown by a dotted line and that over
the 50cm thick one is shown by a broken line, being compared with the
diffraction over the semi-infinite thin barrier at the source side surface by a
continuous line.
Being different from Fig. 3, the transfer functions are not much changed in the low frequency range, but they are similarly decreased in the high frequency range as thickness becomes larger. The foot in the impulse response after the peak is not much changed.
B-5) Diffraction of a semi-infinite thick barrier equivalent to a semi-infinite thin barrier
For a semi-infinite thin barrier, two different equivalent semi-infinite thick barriers are replaced as shown in Fig.5. The width W1 is 10cm and W2 is 50cm. rs and r are 100cm. The diffraction of the two different equivalent thick barriers is shown in Fig. 5, being compared with the diffraction of the semi-infinite thin barrier.
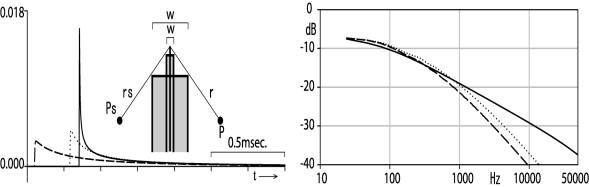
(i) Impulse response (ii) Transfer function
Fig.5 Diffraction of semi-infinite thick
barriers equivalent to a semi-infinite thin barrier, when rs and r
are 100cm
Point source Ps is at (-70.7, 0.0, 70.7) in
cm and a receiving point P is at (-70.7, 0.0, -70.7) in cm. The diffraction of
the semi-infinite 10cm thick barrier is shown by a dotted line, and that of the
50cm thick barrier is shown by a broken line. The diffraction of the semi-infinite
thin barrier is shown by a continuous line.
If thickness is increased, the diffraction becomes less in the high frequency even having its height lower than the thin barrier, but it has similar level in the low frequency. The semi-infinite thin barrier equivalent to a semi-infinite thick barrier gives less diffraction loss in the high frequency.
As they are shown in B-3) ~ 5), if the thickness of a semi-infinite barrier is larger, the peak in the impulse response is lower. However, the successive foot is not much changed and the low frequency components are not much changed except in the case of B-3). The estimation of this difference on loudness is discussed later.
B-6) Diffraction by the increase of wedge number on top of a semi-infinite thick barrier
The diffraction of a semi-infinite thick barrier having a wedge on top in Fig.6 is calculated by the half amplitude method, and is compared with the diffraction of a semi-infinite thick barrier as well as that of a semi-infinite thin barrier in Fig.7 to see how the increase of wedges on top changes diffraction.
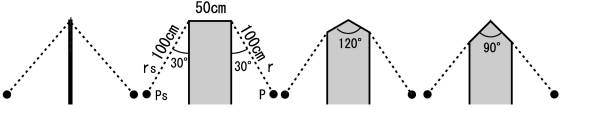
Fig.6 Diffraction of a semi-infinite thick
barrier of various top shapes
The tops of a thin barrier and a wedge barrier are located in the middle point of the thick barrier. The wedge angles are 120degrees and 90degrees. When rs and r are 100cm, and a point source Ps is at (-86.6, 0.0, 50.0) in cm and a receiving point P is at (-86.6, 0.0, -50.0) in cm, the diffraction is shown in Fig.7.
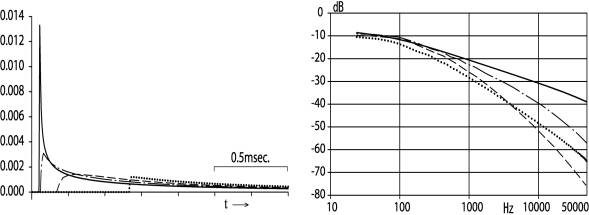
(i) Impulse response (ii) Transfer function
Fig.7 Diffraction of a semi-infinite
barrier of various top shapes when rs and r are 100cm
The diffraction of the thin barrier is
shown by a continuous line, that of the thick barrier
is shown by a dotted line, that of the wedge barrier with a wedge angle
120degrees is shown by a broken line, and that of a wedge with the wedge angle
90degrees is shown by a chained line.
The peak value and the rising point of the impulse response of a semi-infinite thick barrier depend on top shape, and they are decided by their geometrical relation with a point source and a receiving point. A wedge top barrier could be used for a noise barrier using such relationship.
Peak value of an impulse response depending on wedge angle is shown in Fig.8 having a wedge angle on the horizontal axis.
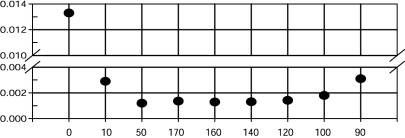
Wedge angle
Fig.8 Peak value of an impulse response
depending on a wedge angle
When the impulse response of our hearing system5) is convolved to it, a thick wedge semi-infinite barrier is more advantageous than a thin semi-infinite barrier.
C) Further possibility of the reduction of noise at the top
The fact that the half amplitude method predicts quite well the measured results shows that the diffraction over a semi-infinite wedge barrier is concentrated on the ridge making a line source. Further, it is the multiple reflections of the first diffracted wave around there. Accordingly, referring to the first diffraction formula, the semi-infinite wedge diffraction has also a row of Delta functions with time delay of the path difference from the source to the receiving point via the ridge.
Porous material is often lined on the top of a thin barrier 7). The impulse response of a porous material layer with the rigid back is indeed a decreasing response as in Fig. 9(i), but all reflections by impedance mismatching are positive.
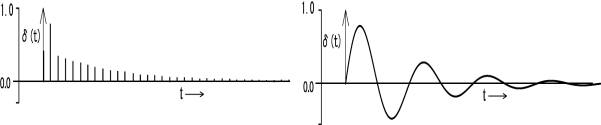
(i)Impulse response of a porous layer (ii) Impulse response of a Helmholz resonator
Fig.9 Schematic expression of the impulse responses of a porous layer and a Helmholz resonator
On the other hand, the impulse response of a resonance absorber, like a Helmholz resonator, is a decreasing response with positive and negative amplitudes with the period of the resonance frequency as shown in Fig. 9(ii). If this system is installed in the first ridge, the convolution of the Delta function row of the diffraction and the impulse response in Fig. 9(ii) decreases the noise over the wedge more effectively than the porous layer. However, the Delta function row has the time delay, careful treatment would be necessary.
References
1) Y. Sakurai and H. Morimoto: “Diffraction of a semi-infinite thick barrier”, Internoise98 , #151, Christchurch(1998), and
H. Morimoto and Y. Sakurai: “Diffraction around a rectangular body”, Internoise98, #176, Christchurch(1998).
2) Y. Sakurai: “The transient response of the sensory systems”, Material for the symposium ‘Physio-psyco dynamics for Architectural environmental designing’, p2-18, Nov.30, 1991, Nagoya( in Japanese).
3) H. Morimoto and Y. Sakurai: ”Diffraction of a semi-infinite thick barrier”, Journal of the Acoust. Soc. of Jp. ( in Japanese), to be published
4) Y. Sakurai and H. Morimoto: ”Diffraction with various noise barrier arrangements”, p47-51, 15th Biennial Conference of The New Zealand Acoustical Society, Sept. 2000.
5) Y. Sakurai and H. Morimoto: ”The transient response of human hearing system”, p221-228. J.A.S.Jp.(1989
6) Y. Sakurai and H. Morimoto: “Binaural hearing and time window in the transient”, p229-233, J.A.S.Jp.(1989).
7) K. Fujiwara and N. Furuta: “Sound shielding efficiency of a barrier with a cylinder at the edge”, Noise Control Engineering Journal, Vol.37, No1, p5-11 (1991).